Prelude: Decibels

You’ve probably heard the term decibel used in conjunction with sound levels: having a muffler louder than 85 dB will get you a ticket, listening to music at 110 dB will damage your hearing. You’ve probably also noticed the button marked ATT -20dB on the function generator, so decibels don’t just have to do with sound. So what exactly is a decibel? It’s a logarithmic way of expressing the ratio of two power levels (or sound pressure levels, or voltage levels, or any other kinds of levels). More precisely,

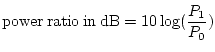$\displaystyle {\rm power\: ratio\: in\: dB} = 10 \log(\frac{P_1}{P_0})$where $P_0$ and $P_1$ are the two powers being compared, and $\log()$ is the common, or base 10 logarithm. If we have two voltage levels, $V_1$ and $V_2$ across the same load resistance, $R_L$ , then

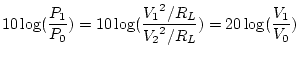$\displaystyle 10 \log(\frac{P_1}{P_0}) = 10 \log(\frac{{V_1}^2/R_L}{{V_2}^2/R_L}) = 20 \log(\frac{V_1}{V_0})$Why logarithmic? The smallest perceivable sound level corresponds to an acoustic power density of approximately $10^{-12}\rm W/m^2$ . But the level at which the sensation of sound begins to give way to the sensation of pain is about $1\rm W/m^2$ . To cope with this large dynamic range without loosing track of the number of zeros after the decimal point, a logarithmic scale is useful.

It’s important to remember that a decibel measurement expresses a ratio. So it always makes sense to say that a signal x is so many dB greater (or less) than signal y. But if we say that a signal is equal to some number of decibels, then there must be a reference level. For sound, that reference level is usually taken as $10^{-12}\rm W/m^2$ which corresponds to a pressure of $10^{-5}\rm N/m^2$ . If we call this the reference pressure level, $p_0$ , we get the definition of sound pressure level

$\displaystyle {\rm SPL} = 20 \log(\frac{p}{p_0})$(where we use 20 instead of 10 since power is proportional to the square of the pressure).

In a circuit, the choice of a reference level is not quite so obvious. For voltages, the typical choice is 1 V, which gives “decibels relative to 1 Volt” or dBV for short. Other forms you may encounter are dBW (relative to 1 watt) or dBm (relative to 1 mW).

It is sometimes stated that the response of a filter falls off at “20dB per decade” or “6dB per octave”. This is just another way of saying that the response varies as 1/f. In other words, if $f_2$ is 10 times $f_1$ (i.e. the frequencies are separated by one decade) then $\vert H(f_2)\vert$ will be 1/10 of $\vert H(f_2)\vert$ . Since$20 \log(1/10) = -20$ then we have a loss of 20dB (or a gain of -20dB) for each decade increase in frequency. Similarly, for two frequencies separated by one octave (a factor of two) we would have $20 \log(1/2) = -6.02$ or approximately 6dB per octave.

For more information, check out the article on Decibels at UCSC Electronic Music Studios.